In January, I did a series with some heavier mathematics, involving lots of number theory, combinatorics, and some fairly difficult manipulation. Last month, we took a little rest from this by talking a bit about casino games and optimal strategies. The mathematics we used was more probability and game theory. This month, I thought we could explore something completely different that is also extremely interesting. It is taught in school (much of the material in this post actually comes straight from my math class), but maybe not in a fun, thought-provoking way. This month, we will dive into trigonometry.
If you want to brush up on your basic foundational trigonometry, please click
here. It is my post on the Law of Cosines, but also explains at the beginning what the sine, cosine, and tangent functions are. I will make sure to prove any other trigonometric identities we use in this series (or link to a proof), so all you need to know is what a sine, cosine, and tangent is.
Now we are ready to derive our first identity. We will try to figure out a simpler way of writing sin(α+β). There are many proofs of this, but I am using one that I found at www.themathpage.com. Let's start with a diagram to help explain this idea.
Create the line AB.
Rotate it to point C, creating the angle α.
Rotate it to point D, creating the angle β.
Draw DE perpendicular to AB.
Draw DF perpendicular to AC.
Draw FG perpendicular to AB.
Draw FH perpendicular to ED.
We are trying to figure out the sine of α+β, which can be written as (ED/DA). First, let's determine the value of the angle HDF (which has already been written in for us).
Note that the lines HF and AG are parallel, with a transversal (a line that intersects both lines) of AF. In geometry, there is a theorem called the Alternate Interior Angle Theorem, that essentially tells us that in this circumstance, the measure of angle GAF is equal to the measure of angle AFH. In other words, angle AFH has a measure of α. Noting that angle AFD has a measure of 90 and AFH has a measure of α, that means angle HFD would have a measure of 90–α. Since a triangle has 180 degrees, having two angle measures in a triangle is enough to get the third. Triangle HFD has an angle of 90, an angle of 90–α, and one more angle that creates a sum of 180 degrees. Do the math and you will find that the angle must be α, and thus, angle HDF has a measure of α as depicted in the diagram.
Now we can try to find the formula. Let's start with the following equality:
ED = GF + HD
Note that we are trying to find what (ED/DA) equals. Because of this, let's divide both sides by DA.
(ED/DA) = (GF/DA) + (HD/DA)
Let's complicate some terms on the right hand side. Multiply the fraction on the left by (AF/AF) and the one on the right by (FD/FD)
(ED/DA) = (GF/AF)(AF/DA) + (HD/FD)(FD/DA)
(ED/DA) is simply the sine of α+β. Looking back at the diagram, (GF/AF) would be the sine of α. (AF/DA) would be the cosine of β. (HD/FD) would be the cosine of α. (FD/DA) would be the sine of β. This gives us the following formula:
sin(α + β) = sinα cosβ + cosα sinβ
This is a beautiful result. The sine of the sum of two quantities can just be pulled apart so easily. This is really cool on its own, and furthermore, it ends up being the foundation of tons more identities. Let's say we wanted to find the sine of α–β. We could just plug (-β) in for β and see what we get.
sin(α – β) = sinα cos(-β) + cosα sin(-β)
These negative terms can be analyzed in a number of ways, but the easiest way to do it is to look at the graphs of the sine and cosine functions.
 |
| Graph of y = sin(x) |
 |
| Graph of y = cos(x) |
Notice how the sine graph is symmetric over the origin. Any sin(x) will equal -sin(-x) and any sin(-x) will equal -sin(x). On the other hand, the cosine graph is symmetric over the y-axis. Any cos(x) will equal cos(-x) and -cos(x) will equal -cos(-x). This enables us to simplify the formula much more.
sin(α – β) = sinα cos(-β) + cosα sin(-β)
sin(α – β) = sinα cosβ + cosα (-sinβ)
sin(α – β) = sinα cosβ – cosα sinβ
Fantastic. What if we wanted to find the cosine of the sum of two angles? Going back to our original diagram, we can start with the following expression:
EA = GA - FH
Dividing through by AD creates the desired left hand side.
(EA/AD) = (GA/AD) - (FH/AD)
Multiply the term on the left of the right hand side by (AF/AF) and the right term by (DF/DF) to get:
(EA/AD) = (GA/AF)(AF/AD) - (FH/DF)(DF/AD)
And turning this into the appropriate functions gives:
cos(α + β) = cosα cosβ – sinα sinβ
Doing the same thing as before gives a subtraction formula of:
cos(α – β) = cosα cosβ + sinα sinβ
Finally, let's try to create a tangent formula. Knowing that dividing the sine by the cosine will give the tangent, let's try dividing the two formulas by each other.
sinα cosβ + cosα sinβ
cosα cosβ – sinα sinβ
Divide each term through by cos
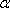
cosβ.
(sinα cosβ)/(cosα cosβ) + (cosα sinβ)/(cosα cosβ)
(cosα cosβ)/(cosα cosβ) – (sinα sinβ)/(cosα cosβ)
Many terms will now cancel.
(sinα)/(cosα) + (sinβ)/(cosβ)
1 – ((sinα)/(cosα))((sinβ)/(cosβ))
Turning the sine and cosine ratios into tangents gives a formula of:
tanα + tanβ
1 – tanα tanβ
And there's the formula! If you wanted to create a subtraction formula, you would just note that the tangent function is symmetric over the origin (or it is an odd function), and plug in the necessary values to get:
tanα – tanβ
1 + tanα tanβ
I think that these are really cool formulas. But they are also very practical. For instance, let's say you want to find the exact sine of 75°. We know that sin(45) = (√2)/2, sin(30) = 1/2, cos(45) = (√2)/2, and cos(30) = (√3)/2. So, this can be determined with the sine angle addition formula.
sin(75) = sin(30 + 45) = sin30cos45 + cos30sin45 = (1/2)((√2)/2) + ((√3)/2)((√2)/2) = (√(2) + √(6))/4
Knowing that the Greeks did some manipulation with the regular pentagon to find an exact sine of 72°, we can plug all of this information into the sine angle subtraction formula to find the exact sine of 3°. We can then eventually make our way down to 1°, which gives us the ability to generate the sines of all of the angles on the trig tables that mathematicians now use today.
Next week, we will use these formulas to create more generalizations that will make many of these trig table computations much much simpler. And give us some really pretty formulas in the process.







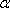 cosβ.
cosβ.